Determining loan amortization schedules, periodic payment amounts, total payment value, or interest
rates can be somewhat complex. To help facilitate these kinds of calculations, GnuCash has a
built-in Loan Repayment Calculator. To access the calculator, go to
→
.
The Loan Repayment Calculator can be used to calculate any one of the parameters: Payment Periods, Interest Rate, Present Value, Periodic Payment, or Future Value given that the other 4 have been defined. You will also need to specify the compounding and payment methods.
Payment Periods - the number of payment periods.
Interest Rate - the nominal interest rate of the loan, ie: the yearly interest rate.
Present Value - the present value of the loan, ie: current amount owed on the loan.
Periodic Payment - the amount to pay per period.
Future Value - the future value of the loan, ie: the amount owed after all payment periods are over.
Compounding - two interest compounding methods exist, discrete or continuous. For discrete compounding select the compounding frequency from the popup menu with a range from yearly to daily.
Payments - the popup menu allows you to select the payment frequency with a range from yearly to daily. You can also select whether your payments occur at the beginning or end of the period. Payments made at the beginning of the payment period have interest applied to the payment as well as any previous money paid or money still owed.
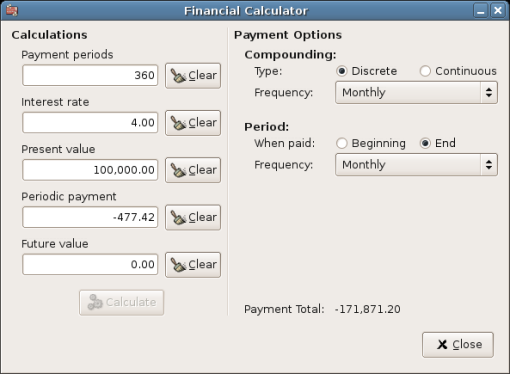
What is your monthly payment on a $100000 30 year loan at a fixed rate of 4% compounded monthly?
This scenario is shown in the example image above. To perform this calculation, set Payment Periods to 360 (12 months x 30 years), Interest Rate to 4, Present Value to 100000, leave Periodic Payment empty and set Future Value to 0 (you do not want to owe anything at the end of the loan). Compounding is Monthly, Payments are Monthly, assume End of Period Payments, and Discrete Compounding. Now, click on the button next to the Periodic Payment area. You should see $-477.42.
Answer: You must make monthly payments of 477.42.
How long will you be paying back a $20000 loan at 10% fixed rate interest compounded monthly if you pay $500 per month?
To perform this calculation, leave Payment Periods empty, set Interest Rate to 10, Present Value to 20000, Periodic Payment is -500, and Future Value is 0 (you do not want to owe anything at the end of the loan). Compounding is Monthly, Payments are Monthly, assume End of Period payments, and Discrete Compounding. Now, click on the . You should see 49 in the Payment Periods field.
Answer: You will pay off the loan in 4 years and 1 month (49 months).
In order to discuss the mathematical formulas used by the Loan Repayment Calculator, we first must define some variables.
n == number of payment periods %i == nominal interest rate, NAR, charged PV == Present Value PMT == Periodic Payment FV == Future Value CF == Compounding Frequency per year PF == Payment Frequency per year Normal values for CF and PF are: 1 == annual 2 == semi-annual 3 == tri-annual 4 == quaterly 6 == bi-monthly 12 == monthly 24 == semi-monthly 26 == bi-weekly 52 == weekly 360 == daily 365 == daily
When a solution for n, PV, PMT or FV is required, the nominal interest rate (i) must first be converted to the effective interest rate per payment period (ieff). This rate, ieff, is then used to compute the selected variable. When a solution for i is required, the computation produces the effective interest rate (ieff). Thus, we need functions which convert from i to ieff, and from ieff to i.
To convert from i to ieff, the following expressions are used: Discrete Interest: ieff = (1 + i/CF)^(CF/PF) - 1 Continuous Interest: ieff = e^(i/PF) - 1 = exp(i/PF) - 1 To convert from ieff to i, the following expressions are used: Discrete Interst: i = CF*[(1+ieff)^(PF/CF) - 1] Continuous Interest: i = ln[(1+ieff)^PF]
 | Примечание |
|---|---|
In the equations below for the financial transaction, all interest rates are the effective interest rate, «ieff». For the sake of brevity, the symbol will be shortened to just «i». | |
One equation fundamentally links all the 5 variables. This is known as the fundamental financial equation:
PV*(1 + i)^n + PMT*(1 + iX)*[(1+i)^n - 1]/i + FV = 0
Where: X = 0 for end of period payments, and
X = 1 for beginning of period paymentsFrom this equation, functions which solve for the individual variables can be derived. For a
detailed explanation of the derivation of this equation, see the comments in the file
src/calculation/fin.c from the GnuCash source code. The A, B, and C variables are defined
first, to make the later equations simpler to read.
A = (1 + i)^n - 1 B = (1 + iX)/i C = PMT*B n = ln[(C - FV)/(C + PV)]/ln((1 + i) PV = -[FV + A*C]/(A + 1) PMT = -[FV + PV*(A + 1)]/[A*B] FV = -[PV + A*(PV + C)] The solution for interest is broken into two cases. The simple case for when PMT == 0 gives the solution: i = [FV/PV]^(1/n) - 1
The case where PMT != 0 is fairly complex and will not be presented here. Rather than involving an exactly solvable function, determining the interest rate when PMT !=0 involves an iterative process. Please see the src/calculation/fin.c source file for a detailed explanation.
Let’s recalculate Раздел 8.3.1, «Example: Monthly Payments», this time using the mathematical formulas rather than the Loan Repayment Calculator. What is your monthly payment on a $100000 30 year loan at a fixed rate of 4% compounded monthly?
First, let’s define the variables: n = (30*12) = 360, PV = 100000, PMT = unknown, FV = 0, i = 4%=4/100=0.04, CF = PF = 12, X = 0 (end of payment periods).
The second step is to convert the nominal interest rate (i) to the effective interest rate (ieff). Since the interest rate is compounded monthly, it is discrete, and we use: ieff = (1 + i/CF)^(CF/PF) - 1, which gives ieff = (1 + 0.04/12)^(12/12) - 1, thus ieff = 1/300 = 0.0033333.
Now we can calculate A and B. A = (1 + i)^n - 1 = (1 + 1/300)^360 - 1 = 2.313498. B = (1 + iX)/i = (1 + (1/300)*0)/(1/300) = 300.
With A and B, we can calculate PMT. PMT = -[FV + PV*(A + 1)]/[A*B] = -[0 + 100000*(2.313498 + 1)] / [2.313498 * 300] = -331349.8 / 694.0494 = -477.415296 = -477.42.
Answer: You must make monthly payments of 477.42.